배열
원소 하나를 저장하고 검색하는데 평균 O(n)의 시간 소요
트리
원소하나를 저장하고 검색하는 데 평균 O(log n)의 시간 소요
저장된 자료의 양에 상관없이 원소 하나를 저장하고 검색하는 것을 상수 시간에 가능하게 할수는 없을까?
해시테이블?!
임의의 원소를 해시테이블에 저장하려면
1. 해당 원소의 해식밧을 해시 함수를 이용하용 계산한다.
2. 이 해시값을 주소로 하는 위치에 원소를 저장한다.
3. 저장 후에 검색을 할때도 원소의 해시값을 계산해 바로 해당 위치로 이동한다.
해시테이블은 원소의 저장된 위치를 상수시간에 계산할 수 있다.
해시 함수
임의의 길이를 데이터를 고정된 길이의 데이터로 매핑하는 함수
좋은 해시 함수의 조건
계산이 간단해야 한다
입력 원소가 해시테이블 전체에 고루 저장되어야 한다
해시 충돌
해시 함수가 서로 다른 두개의 입력 값에 대해 같은 출력값을 내는 상황
해결방안 1: 체이닝(Chaning)
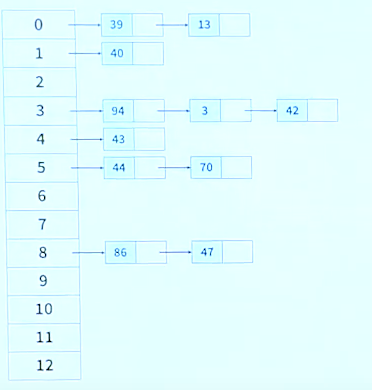
같은 주소로 해싱되는 원소를 모두 하나의 연결리스트에 매달아서 관리한다
원소를 검색할 때는 해당 연결리릇트의 원소들을 차례로 지나가면서 탐색한다
해결방안 2: 개방 주소 방법(Open addressing)
체이닝과 달리 어떻게든 주어진 테이블 공간에서 해결한다.
따라서 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없다.
선형 조사(linear probing), 이차원 조사(quadratic probing) ,더블 해싱(double hashing)
선형 조사(linear probing)
가장 간단한 해결 충돌 방법
충동이 일어난 자리에서 i에 관한 일차 함수의 보폭으로 점프한다 -> 넘어간다
hi(x)는 h(x)에서 i 만큼 떨어진 자리 이다.
테이블의 경계를 넘어갈 경우에는 맨앞으로 돌아간다
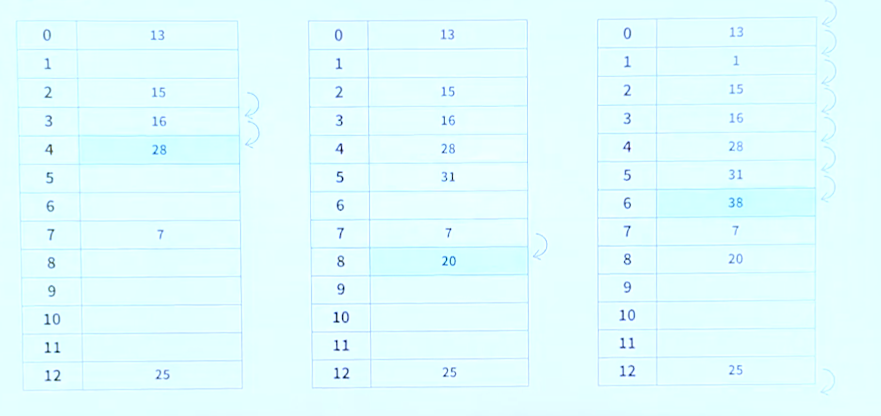
이차원 조사(quadratic probing)
바로 뒷자리를 보는 대신 보폭을 이차함수로 넓혀가면서 본다
예를 들어 i 번째 해시 함수를 h(x)에서 i**2만큼 떨어진 자리로 삼는다.
즉 h(x), h(x)+1, h(x)+4, h(x)+ 9.........
특정 영역에 원소가 몰려도 그 영역을 빨리 벗어날수 있다.

더블 해싱(double hashing)
두개의 함수를 사용한다.
하나의 함수는 최초의 해시값을 얻을 때, 다른 하나의 함수는 해시충돌이 일어났을 때 이동할 폭을 얻을 때 사용한다.
두 원소의 첫번째 해시값이 같더라도 두번째 해시값까지 같은 확률은 매우 작으므로 서로 다른 보폭으로 점프를 하게된다.
해심 함수의 특징
같은 입력값에 대해서 같은 출력값이 보장된다.
서로 다른 입력값으로부터 동일한 출력값이 나올 가능성이 희박하므로 입력값에 대한 무결성이 보장된다
일방향성을 갖는다.
해시 알고리즘
SHA(Secure Hash Algorithm)
NSA에 의해 1993년 처음 개발된 해시 알고리즘
현재 주로 사용되는 것을 SHA-2 함수 군으로 , 다이제스트의 길이에 따라 SHA-256, SHA-512등으로 나뉜다
SHA-0, SHA-1 까지는 해시 충돌성이 존재하지만 SHA-256, SHA-516는 해시 충돌성이 사실상 0에 수렴
256의 의미: 해싱을 하면 2**256개의 해시값 중 하나가 나타난다
해시의 응용
무결성 검사
클라우드 스토리지에서 동일한 파일 식별 및 수정된 파일 검출
데이터베이스에 비밀번호를 저장할 때 사용
블록체인
Git
www.youtube.com/watch?v=Rpbj6jMYKag&list=PLgXGHBqgT2TvpJ_p9L_yZKPifgdBOzdVH&index=87